
Confidence limitsâfrom the dichotomous test decision to the effect range estimate. This range, with a certain level Doing so invariably creates a broader range, as it makes room for a greater number of sample means. A Confidence interval (CI) is an interval of good estimates of the unknown true population parameter.About a 95% confidence interval for the mean, we can state that if we would repeat our sampling process infinitely, 95% of the constructed confidence intervals would contain the true population mean. A 99% confidence interval for the proportion in the whole population having the same intention on the survey might be 30% to 50%. The confidence interval gives us a range of reasonable values for the difference in population means μ 1 â μ 2. Doing so invariably creates a broader range, as it makes room for a greater number of sample means. The confidence interval(CI) for the difference between the two population means is used to assist researchers in questions such as these. This gives a rule such that, if applied repeatedly to similar problems, the 95% confidence interval will contain the true parameter value in 95% of the cases. If you calculate a confidence interval with a 95% confidence level, it means that you are confident that 95 out of 100 times your estimated results will fall between the upper and lower values. One-sided and two-sided intervals are supported, as well as confidence intervals for relative difference (percent difference). When we assume equal variances we need to "pool" the two standard deviation. For example, if you are estimating a 95% confidence interval around the mean proportion of female babies born every year based on a random sample of babies, you might find an upper bound of 0.56 and a lower bound of 0.48. That means the two fats might have the same or different absorption, so you canât say whether thereâs a difference.
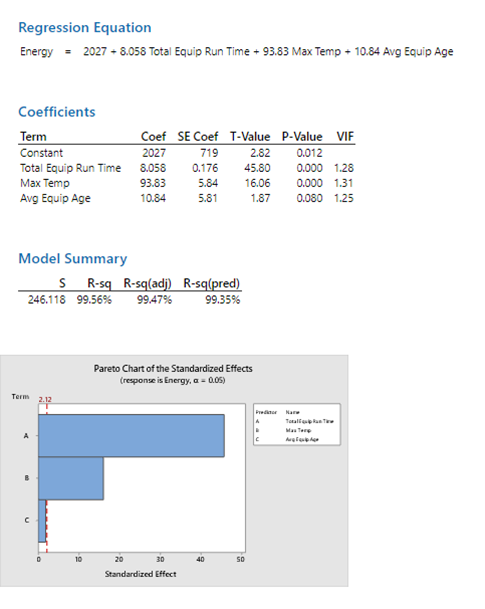
For example, a confidence interval can be used to describe how reliable survey results are. The confidence interval is the actual upper and lower bounds of the estimate you expect to find at a given level of confidence. The form of the confidence interval is similar to others we have seen. For these two problems we will estimate this parameter with the sample standard deviation. The confidence intervals for the difference in means provide a range of likely values for (μ 1-μ 2). To calculate the confidence interval, one needs to set the confidence level as 90%, 95%, or 99%, etc. The confidence interval for the difference between Fat 1 and Fat 2 goes from a negative to a positive, so it does include zero. Bootstrap Confidence Intervals Randomization Hypothesis Tests One Quantitative Variable: CI for Single Mean, Median, St.Dev. The extreme difference in interval values would allow us to sa The formula for estimation is: A confidence interval gives upper and lower bounds on the range of parameter values you might expect to get if we repeat our measurements. The confidence interval is a range of values calculated by statistical methods which includes the desired true parameter (for example, the arithmetic mean, the difference between two means, the odds ratio etc.) The TI 83 allows you to find a CI for the difference between two means in a matter of a few keystrokes. The confidence interval for the difference in means - is given by where t * is the upper (1- C )/2 critical value for the t distribution with k degrees of freedom (with k equal to either the smaller of n 1 -1 and n 1 -2 or the calculated degrees of freedom). To find the confidence interval from this, look up the confidence level you want to calculate the interval for in a Z -score table and multiply this value by the Z score. Assuming equal variances, a 90% confidence interval completed for a difference of two means, yielded an interval of (-1243.754, -86.255). The confidence interval for the difference in means provides an estimate of the absolute difference in means of the outcome variable of interest between the comparison groups.
95% Confidence Interval For the Difference.Purchase Access.


 0 kommentar(er)
0 kommentar(er)
